问题
解答题
已知椭圆9x2+16y2=144，焦点为F1、F2，P是椭圆上一点， 且∠F1PF2=60°，求△PF1F2的面积．
答案
解：由题意得椭圆方程为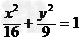
，
∴a=4，b=3，c=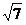
，
在△PF1F2中，
由余弦定理得4c2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos60°=|PF1|2+|PF2|2-|PF1|·|PF2|=(|PF1|+|PF2|)2-3|PF1|·|PF2|,
又∵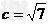
,|PF1|+|PF2|=2a=8,
∴|PF1|·|PF2|=12,
