问题
解答题
甲、乙两个商场出售相同的某种商品，每件售价均为3000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一件按原售价收费，其余每件优惠30%；乙商场的优惠条件是：每件优惠25%．设所买商品为x件时，甲商场收费为y1元，乙商场收费为y2元．
（1）分别求出y1，y2与x之间的关系式；
（2）当甲、乙两个商场的收费相同时，所买商品为多少件？
（3）当所买商品为5件时，应选择哪个商场更优惠？请说明理由．
答案
（1）
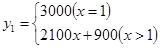；y2=2250x；
（2）甲、乙两个商场的收费相同时，所买商品为6件；
（3）所买商品为5件时，应选择乙商场更优惠．
题目分析：（1）由两家商场的优惠方案分别列式整理即可；
（2）由收费相同，列出方程求解即可；
（3）由函数解析式分别求出x=5时的函数值，即可得解
试题解析：（1）当x=1时，y1=3000；
当x＞1时，y1=3000+3000（x﹣1）×（1﹣30%）=2100x+900．
∴；
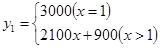y2=3000x（1﹣25%）=2250x，
∴y2=2250x；
（2）当甲、乙两个商场的收费相同时，2100x+900=2250x，
解得x=6，
答：甲、乙两个商场的收费相同时，所买商品为6件；
（3）x=5时，y1=2100x+900=2100×5+900=11400，
y2=2250x=2250×5=11250，
∵11400＞11250，
∴所买商品为5件时，应选择乙商场更优惠．