问题
解答题
已知椭圆E的方程为2x2+y2=2,过椭圆E的一个焦点的直线l交椭圆于A、B两点。
(1)求椭圆E的长轴和短轴的长,离心率,焦点和顶点的坐标;
(2)求△ABO(O为原点)的面积的最大值。
答案
解:(1)将椭圆E的方程化为标准方程: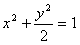
于是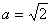 ,
,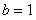 ,
,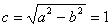
因此,椭圆E的长轴长为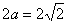 ,短轴长为
,短轴长为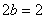 ,离心率
,离心率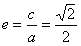 ,两
,两
个焦点坐标分别是F1(0,-1)、F2(0,1),
四个顶点的坐标分别是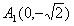 ,
,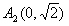 ,
,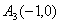 和
和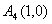 。
。
(2)依题意,不妨设直线l过F2(0,1)与椭圆E的交点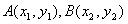
则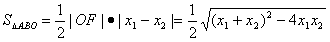
根据题意,直线l的方程可设为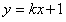
将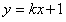 代入
代入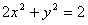 得
得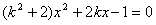
由韦达定理得: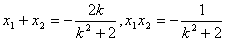
所以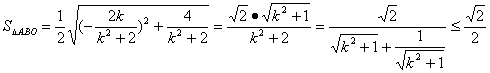
(当且仅当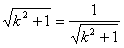 ,即
,即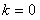 时等号成立)
时等号成立)
故△ABO的面积的最大值为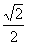 。
。
