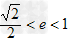问题
解答题
设椭圆上存在一点P ,它到椭圆中心和长轴一个端点的连线互相垂直,求椭圆离心率的取值范同.
答案
解:不妨设椭圆方程为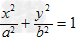 (a>b>0),O为椭圆中心,A(a,0)为右顶点,P(x0,y0).
(a>b>0),O为椭圆中心,A(a,0)为右顶点,P(x0,y0).
∵PO⊥PA,
∴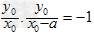 ,
,
即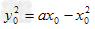
又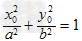
∴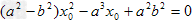 ,
,
即(x0-a)[(a2-b2)x0-ab2]=0.
又0<x0<a,
∴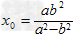 ,且
,且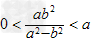 ,
,
而b2= a2-c.
∴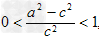
∴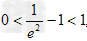
∴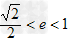
设椭圆上存在一点P ,它到椭圆中心和长轴一个端点的连线互相垂直,求椭圆离心率的取值范同.
解:不妨设椭圆方程为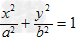 (a>b>0),O为椭圆中心,A(a,0)为右顶点,P(x0,y0).
(a>b>0),O为椭圆中心,A(a,0)为右顶点,P(x0,y0).
∵PO⊥PA,
∴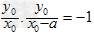 ,
,
即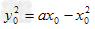
又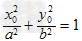
∴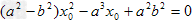 ,
,
即(x0-a)[(a2-b2)x0-ab2]=0.
又0<x0<a,
∴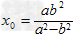 ,且
,且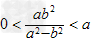 ,
,
而b2= a2-c.
∴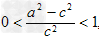
∴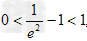
∴