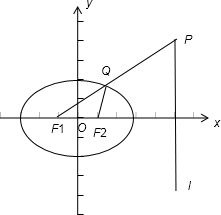
如图F₁（-1，0）、F₂（1，0），右准线l方程x=5，

∵2

F1P

+3

PQ

=

0

，∴

F1Q

+

QP

=

3

2

 

QP

，

∴

F1Q

=

1

2

 

QP

，QP=2QF₁，∴点 Q 分有向线段F₁P 成的比为λ=

1

2

，

设 Q（m，n），则由定比分点坐标公式得m=

-1+ 1 2 ×5

1+ 1 2

=1，

把Q（m，n）代入椭圆的方程得 n=±

4 5

5

，

∴|QF₂|=

4 5

5

，

故选B．