问题
解答题
已知点P是椭圆C:
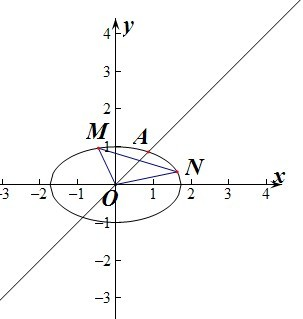
(Ⅰ)求椭圆C的方程及离心率; (Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使
|
答案
(Ⅰ)设P(x0,y0),F1(-c,0),F2(c,0)由|OP|=
,得x02+y02=10 2
,…(1分)5 2
由
•PF1
=PF2
得(-c-x0,-y0)⋅(c-x0,-y0)=1 2
,即x02+y02-c2=1 2
…(2分)1 2
所以c=
,又因为短轴长为2,所以b=1,所以离心率e=2
=c a
,…(4分)6 3
椭圆C的方程为:
+y2=1;…(6分)x2 3
(Ⅱ)解法一:由
得A(y=x
+y2=1x2 3
,3 2
),设直线MN的方程为y=kx+m,3 2
联立方程组
消去y得:(1+3k2)x2+6kmx+3m2-3=0…(7分)y=kx+m
+y2=1x2 3
设M(x1,y1),N(x2,y2),则x1+x2=-
,x1x2=6km 1+3k2
…(8分)3m2-3 1+3k2
所以y1+y2=k(x1+x2)+2m=
.2m 1+3k2
因为
+OM
=λON
,λ∈(0,2),所以x1+x2=OA
λ,y1+y2=3 2
λ,3 2
得kMN=-
,m=1 3
λ,于是x1+x2=3 3
,x1x2=3m 2
…(9分)9m2-9 4
所以|MN|=
|x1-x2|=1+(-
)21 3 10 3
=(x1+x2)2-4x1x2
…(10分)
⋅10 4-3m2 2
又因为λ>0,原点O到直线MN的距离为d=
所以S△OMN=3
m10 10
|MN|d=1 2
⋅
⋅10 4-3m2 4
S△OMN=3
m10 10
|MN|d=1 2
⋅
⋅10 4-3m2 4
=3
m10 10
≤
⋅3 (4-3m2)3m2 4
,3 2
当m=
,即λ=6 3
时等号成立,S△OMN的最大值为2
…(13分)3 2
