问题
填空题
椭圆
|
答案
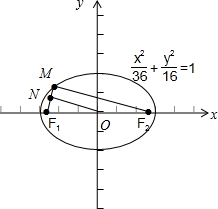
∵椭圆的方程为：
+x2 36
=1，其上一点M到左焦点F1的距离为2，连接MF2，y2 16
∴由椭圆的定义得|MF1|+|MF2|=2a=12，又|MF1|=2，
∴|MF2|=10．
在△MF1F2中，由三角形中位线的性质得，ON∥ .
MF2，1 2
∴|ON|=5．
故答案为：5．
搜题请搜索小程序“爱下问搜题”
椭圆
|
∵椭圆的方程为：
+x2 36
=1，其上一点M到左焦点F1的距离为2，连接MF2，y2 16
∴由椭圆的定义得|MF1|+|MF2|=2a=12，又|MF1|=2，
∴|MF2|=10．
在△MF1F2中，由三角形中位线的性质得，ON∥ .
MF2，1 2
∴|ON|=5．
故答案为：5．