问题
填空题
设椭圆C:
|
答案
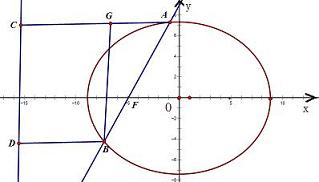
如图,设设椭圆的左准线为l,过A点作AC⊥l于C,
过点B作BD⊥l于D,再过B点作BG⊥AC于G,
直角△ABG中,∠BAG=60°,所以AB=2AG,…①
由圆锥曲线统一定义得:e=
=AF AC
,BF BD
∵|
|=2|AF
|FB
∴AC=2BD
直角梯形ABDC中,AG=AC-BD=
AC…②1 2
①、②比较,可得AB=AC,
又∵AF=
AB2 3
∴e=
=AF AC
=AF AB 2 3
所求的离心率为
.2 3
故答案为:
.2 3
