问题
解答题
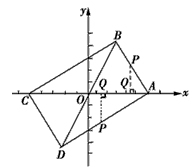
在直角坐标系中,点A(5,0)关于原点O的对称点为点C。
(1)请直接写出点C的坐标;
(2)若点B在第一象限内,∠OAB=∠OBA,并且点B关于原点O的对称点为点D。
①试判断四边形ABCD的形状,并说明理由;
②现有一动点P从B点出发,沿路线BA-AD以每秒1个单位长的速度向终点D运动,另一动点Q从A点同时出发,沿AC方向以每秒0.4个单位长的速度向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动.已知AB=6,设点P、Q的运动时间为t秒,在运动过程中,当动点Q在以PA为直径的圆上时,试求t的值。
答案
解:(1)C(-5,0);
(2)①四边形ABCD为矩形,理由如下:
如图,由已知可得:A、O、C在同一直线上,且 OA=OC;B、O、D在同一直线上,且OB=OD,
∴四边形ABCD是平行四边形,
∵∠OAB=∠OBA
∴OA=OB,即AC=2OA=2OB=BD
∴四边形ABCD是矩形;
②如图,由①得四边形ABCD是矩形
∴∠CBA=∠ADC=90°
又AB=CD=6,AC=10
∴由勾股定理,得BC=AD=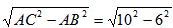 =8
=8
∵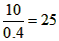 ,
,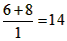 ,
,
∴0≤t≤14
当0≤t≤6时,P点在AB上,连结PQ
∵AP是直径,
∴∠PQA=90°
又∠PAQ=∠CAB,
∴△PAQ∽△CAB
∴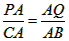 ,
,
即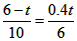 ,
,
解得t=3.6
当6<t≤14时,P点在AD上,连结PQ,同理得∠PQA=90°,△PAQ∽△CAD
∴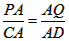 ,
,
即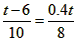 t-6,
t-6,
解得t=12,
综上所述,当动点Q在以PA为直径的圆上时,t的值为 3.6或12。