问题
选择题
设偶函数f(x)在(0,+∞)上为减函数,且f(2)=0,则不等式
|
答案
∵f(x)是偶函数
∴f(-x)=f(x)
不等式
>0,即f(x)+f(-x) x
>02f(x) x
也就是xf(x)>0
①当x>0时,有f(x)>0
∵f(x)在(0,+∞)上为减函数,且f(2)=0
∴f(x)>0即f(x)>f(2),得0<x<2;
②当x<0时,有f(x)<0
∵-x>0,f(x)=f(-x)<f(2),
∴-x>2⇒x<-2
综上所述,原不等式的解集为:(-∞,-2)∪(0,2)
故选B

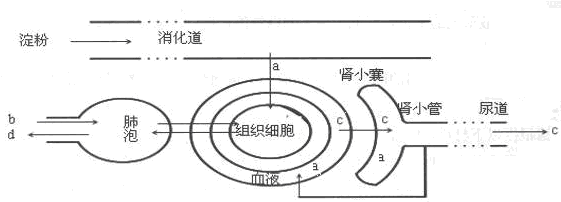 (1)血液循环的动力器官是 _________。
(1)血液循环的动力器官是 _________。