根据题意过点P作PH垂直于x轴，并且交x轴与点H，过点P作PE垂直于右准线，并且交右准线与点E，如图所示：

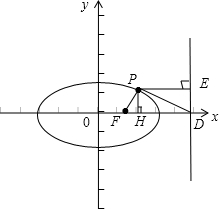
由图象可得：∠DPE=∠PDF．

由椭圆的第二定义可得：

|PF|

|PE|

=e，

因为∠PFD=60°，

所以在△PFH中，|PH|=|PF|sin∠PFD=

3

2

|PF|，

在△PDE中，|DE|=|PE|tan∠DPE=

3

4

|PE|，

因为|PH|=|ED|，

所以

3

2

|PF|=

3

4

|PE|，

所以e=

|PF|

|PE|

=

3

2

．

故答案为：

3

2

．