已知椭圆x225+y216=1内有两点A（1，3），B（3，0），P为椭圆上一点

问题填空题

已知椭圆

=1内有两点A（1，3），B（3，0），P为椭圆上一点，则|PA|+|PB|的最大值为______．

答案

∵椭圆方程为

=1，

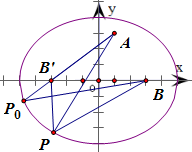
∴焦点坐标为B（3，0）和B'（-3，0）

连接PB'、AB'，根据椭圆的定义，得|PB|+|PB'|=2a=10，可得|PB|=10-|PB'|

因此，|PA|+|PB|=|PA|+（10-|PB'|）=10+（|PA|-|PB'|）

∵|PA|-|PB'|≤|AB'|

∴|PA|+|PB|≤10+|AB'|=10+

(1+3)2+(3-0)2

=10+5=15

当且仅当点P在AB'延长线上时，等号成立

综上所述，可得|PA|+|PB|的最大值为15

故答案为：15