已知△ABC的顶点A,B在椭圆x2+3y2=4上,C在直线l:y=x+2上,且AB∥l.
(Ⅰ)当AB边通过坐标原点O时,求AB的长及△ABC的面积;
(Ⅱ)当∠ABC=90°,且斜边AC的长最大时,求AB所在直线的方程.
(Ⅰ)因为AB∥l,且AB边通过点(0,0),所以AB所在直线的方程为y=x.
设A,B两点坐标分别为(x1,y1),(x2,y2).
由
得x=±1.x2+3y2=4 y=x
所以|AB|=
|x1-x2|=22
.2
又因为AB边上的高h等于原点到直线l的距离.
所以h=
,S△ABC=2
|AB|•h=2.1 2
(Ⅱ)设AB所在直线的方程为y=x+m,
由
得4x2+6mx+3m2-4=0.x2+3y2=4 y=x+m
因为A,B在椭圆上,
所以△=-12m2+64>0.
设A,B两点坐标分别为(x1,y1),(x2,y2),
则x1+x2=-
,x1x2=3m 2
,3m2-4 4
所以|AB|=
|x1-x2|=2
.32-6m2 2
又因为BC的长等于点(0,m)到直线l的距离,即|BC|=
.|2-m| 2
所以|AC|2=|AB|2+|BC|2=-m2-2m+10=-(m+1)2+11.
所以当m=-1时,AC边最长,(这时△=-12+64>0)
此时AB所在直线的方程为y=x-1.

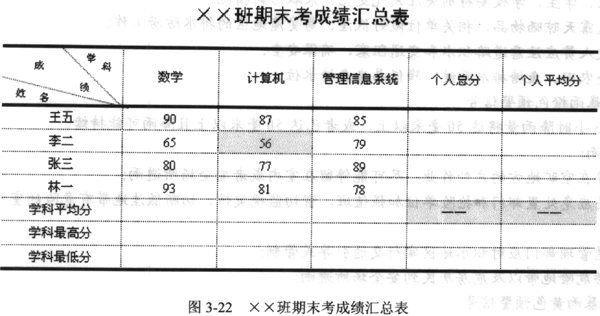 [要求] 1.绘制的成绩汇总表的样式、线条形状、线条颜色与所给图示一致。 2.将表格外部边框线条设置为2.25磅、黑色,线型与图示保持一致;内部线条设置为1磅、黑色,线型与图示保持一致;表头中斜线样式为圆点状虚线、0.75磅、黑色。 3.表格标题文字设置为黑体、黑色、四号、居中,段前、段后间距均为0.5行;表头行添加灰色-12.5%的底纹;表格内所有文字设置为:中文字体为宋体,西文字体为Times New Roman,黑色、小五号、中部居中;斜线表头中的文字大小设置为六号。 4.利用Word内置的函数计算出图3-22中空缺的个人总分、个人平均分、学科平均分、学科最高分和学科最低分。 5.将[成绩]列中分数低于60分的成绩字体颜色设置为红色;将个人总分最高的学生行中的分数字体颜色设置为蓝色、加粗。
[要求] 1.绘制的成绩汇总表的样式、线条形状、线条颜色与所给图示一致。 2.将表格外部边框线条设置为2.25磅、黑色,线型与图示保持一致;内部线条设置为1磅、黑色,线型与图示保持一致;表头中斜线样式为圆点状虚线、0.75磅、黑色。 3.表格标题文字设置为黑体、黑色、四号、居中,段前、段后间距均为0.5行;表头行添加灰色-12.5%的底纹;表格内所有文字设置为:中文字体为宋体,西文字体为Times New Roman,黑色、小五号、中部居中;斜线表头中的文字大小设置为六号。 4.利用Word内置的函数计算出图3-22中空缺的个人总分、个人平均分、学科平均分、学科最高分和学科最低分。 5.将[成绩]列中分数低于60分的成绩字体颜色设置为红色;将个人总分最高的学生行中的分数字体颜色设置为蓝色、加粗。