问题
解答题
设数列{an}的前n项和为Sn，a1=1，an=
（1）求证：数列{an}为等差数列，并分别写出an和Sn关于n的表达式； （2）设数列{
（3）是否存在自然数n，使得S1+
|
答案
（1）证明：由an=
+2（n-1），得Sn=nan-2n（n-1）（n∈N*）．Sn n
当n≥2时，an=Sn-Sn-1=nan-（n-1）an-1-4（n-1），即an-an-1=4，
∴数列{an}是以a1=1为首项，4为公差的等差数列．
于是，an=4n-3，Sn═2n2-n（n∈N*）．
（2）证明：∵
=1 anan+1
=1 (4n-3)(4n+1)
(1 4
-1 4n-3
)，1 4n+1
∴Tn=
+1 a1a2
+…+1 a2a3
=1 anan+1
[（1-1 4
）+（1 5
-1 5
）+（1 9
-1 9
）+…+（1 13
-1 4n-3
）]=1 4n+1
（1-1 4
）＜1 4n+1
，1 4
又易知Tn单调递增，
故Tn≥T1=
=1 a1a2
，1 5
所以
≤Tn＜1 5
．1 4
（3）由Sn=nan-2n（n-1），得
=an-2（n-1）=2n-1（n∈N*），Sn n
∴S1+
+S2 2
+…+S3 3
-（n-1）2=1+3+5+7+…+（2n-1）-（n-1）2Sn n
=n2-（n-1）2=2n-1．
令2n-1=2011，得n═1006，
即存在满足条件的自然数n=1006．
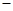、SO42-、Fe3+、H+、M，其物质的量浓度之比
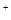）︰c（M）＝5︰3︰2︰3︰2，则M可能是( )