问题
问答题
设3a2-5b<0,讨论方程x5+2ax3+3bx+4c=0的实根个数。
答案
参考答案:
设f(x)=x5+2ax3+3bx+4c,f(x)的定义域为(-∞,+∞),则
f′(x)=5x4+6ax2+3b,
令f′(x)=0,由于判别式
Δ=36a2=60b-12(3a2-5b)<0,可知f′(x)=0无解,即对于任意实数x,f′(x)>0.故f(x)为单调增函数。
又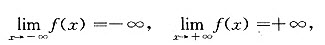
所以f(x)有唯一零点,即原方程有唯一实根.
