（I）

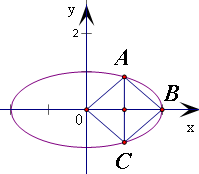
∵四边形OABC为菱形，B是椭圆的右顶点（2，0）

∴直线AC是BD的垂直平分线，可得AC方程为x=1

设A（1，t），得

12

4

+t2=1，解之得t=

3

2

（舍负）

∴A的坐标为（1，

3

2

），同理可得C的坐标为（1，-

3

2

）

因此，|AC|=

3

，可得菱形OABC的面积为S=

1

2

|AC|•|B0|=

3

；

（II）∵四边形OABC为菱形，∴|OA|=|OC|，

设|OA|=|OC|=r（r＞1），得A、C两点是圆x²+y²=r²

与椭圆W：

x2

4

+y2=1的公共点，解之得

3x2

4

=r²-1

设A、C两点横坐标分别为x₁、x₂，可得A、C两点的横坐标满足

x₁=x₂=

2 3

3

•

r2-1

，或x₁=

2 3

3

•

r2-1

且x₂=-

2 3

3

•

r2-1

，

①当x₁=x₂=

2 3

3

•

r2-1

时，可得若四边形OABC为菱形，则B点必定是右顶点（2，0）；

②若x₁=

2 3

3

•

r2-1

且x₂=-

2 3

3

•

r2-1

，则x₁+x₂=0，

可得AC的中点必定是原点O，因此A、O、C共线，可得不存在满足条件的菱形OABC

综上所述，可得当点B不是W的顶点时，四边形OABC不可能为菱形．