问题
问答题
设f（x）=x3+ax2+bx在x=1处有极值-2，试确定a，b的值，并指出f（x）的凹凸区间。
答案
参考答案：
由极值的必要条件有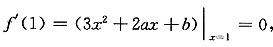
即2a+b=-3．
又极值f(1)=-2，即a+b=-3，解得a=0，b=-3．
于是f(x)=x3-3x，可得f′(x)=3x2-3，f″(x)=6x. 当x＜0时，f″(x)＜0；
当x＞0时，f″(x)＞0，所以f(x)有拐点(0，0)．f(x)的上凸区间为(-∞，0)，下凸区间为(0，+∞)．
