问题
问答题
已知函数f(x)=ax3-6ax2+b(a＞0)在区间[-1，2]上的最大值为3，最小值为-29，求a，b的值。
答案
参考答案：
f′(x)=3ax2-12ax=3ax(x-4).
令f′(x)=0，得驻点x=0或x=4．因为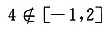
，故舍去x=4．又f(-1)=-7a+b，f(0)=b，f(2)=-16a+b，
因为a＞0，可知f(0)＞f(-1)＞f(2)，
即f(x)在x=0处有最大值，在x=2处取得最小值，所以，最大值f(0)=b=3．最小值f(2)=-16a+b=-29. 解得a=2．