参考答案：

设f(x)=e^x-λx，定义域为(-∞，+∞)．令f′(x)=e^x-λ=0，得驻点x=lnλ，其中λ＞0，因x＞lnλ时，f′(x)＞0；而x＜lnλ时，f′(x)＜0，可知f(x)在x=lnλ处有最小值f(lnλ)=λ(1-lnλ).于是，当1-lnλ＞0，即0＜λ＜e时，f(x)无零点，即方程e^x=λx无解；当1-lnλ=0，即λ=e时，f(lne)=f(1)=0，方程e^x=λx有解x=1；当1-lnλ＜0，即λ＞e时，f(lnλ)＜0，而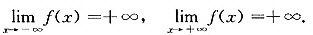

所以f(x)在(-∞，lnλ)内单调减，f(x)在(-∞，lnλ)内有一实根．而f(x)在(lnλ，+∞)内单调增，f(x)在(lnλ，+∞)内也有一实根．