问题
单项选择题
设f(x)存在二阶连续导数,且满足xf″(x)+3x[f′(x)]2=1-e-x,又x0为驻点,则()。
A.f(x0)为f(x)的极大值
B.f(x0)为f(x)的极小值
C.(x0,f(x0))为f(x)的拐点
D.f(x0)非极值,(x0,f(x0))也非拐点
答案
参考答案:B
解析:
因为f′(x0)=0,所以x0f″(x0)=1-e-x0,即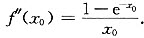
已知f″(x)连续,故x0≠0.而当x0<0时,e-x0>1,有f″(x0)>0;当x0>0时,e-x0<1,有f″(x0)>0.故在x0处函数f(x)必有极小值.故应选B.
