问题
填空题
已知⊙O的半径为2，弦AB的长也是2，则∠AOB=______，弦心距为______．
答案
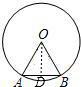
如图所示，OA=OB=AB=2，
∵OA=OB=AB=2，
∴△OAB是等边三角形，
∴∠AOB=60°，
过O作OD⊥AB于D，则OD=OA?sin∠OAB=2×
=3 2
．3
∴弦心距为
．3
故答案为：60°，
．3
搜题请搜索小程序“爱下问搜题”
已知⊙O的半径为2，弦AB的长也是2，则∠AOB=______，弦心距为______．
如图所示，OA=OB=AB=2，
∵OA=OB=AB=2，
∴△OAB是等边三角形，
∴∠AOB=60°，
过O作OD⊥AB于D，则OD=OA?sin∠OAB=2×
=3 2
．3
∴弦心距为
．3
故答案为：60°，
．3