问题
填空题
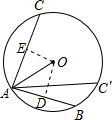
已知⊙O的半径OA=1,弦AB、AC的长分别是
|
答案
分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,根据垂径定理得AE=
AC=1 2
,AD=3 2
AB=1 2
,2 2
∴sin∠AOE=
=AE AO
=3 2 1
,sin∠AOD=3 2
=AD OA
,2 2
根据特殊角的三角函数值可得∠AOE=60°,∠AOD=45°,
∴∠BAO=45°,∠CAO=90°-60°=30°,
∴∠BAC=45°+30°=75°,
或∠BAC′=45°-30°=15°.
故答案为:15°或75°.

 。
。 。
。