问题
选择题
已知正方形ABCD的顶点A,B为椭圆的焦点,顶点C,D在椭圆上,则此椭圆的离心率为( )
|
答案
解:设椭圆方程为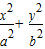 =1,(a>b>0)
=1,(a>b>0)
∵正方形ABCD的顶点A,B为椭圆的焦点,
∴焦距2c=AB,其中c= 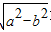 >0
>0
∵BC⊥AB,且BC=AB=2c
∴AC=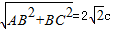 根据椭圆的定义,可得2a=AC+BC=2
根据椭圆的定义,可得2a=AC+BC=2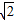 c+2c
c+2c
∴椭圆的离心率e=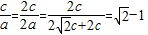
故选A
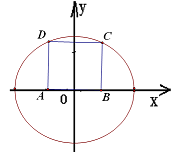
已知正方形ABCD的顶点A,B为椭圆的焦点,顶点C,D在椭圆上,则此椭圆的离心率为( )
|
解:设椭圆方程为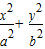 =1,(a>b>0)
=1,(a>b>0)
∵正方形ABCD的顶点A,B为椭圆的焦点,
∴焦距2c=AB,其中c= 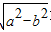 >0
>0
∵BC⊥AB,且BC=AB=2c
∴AC=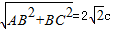 根据椭圆的定义,可得2a=AC+BC=2
根据椭圆的定义,可得2a=AC+BC=2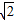 c+2c
c+2c
∴椭圆的离心率e=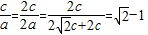
故选A
