参考答案：由题设知X的概率密度为

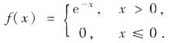
若记A=“通话时间超过6分钟”，则A={X＞6}，

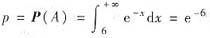．如果用Y表示“800人次通话中通话时间超过6分钟”的次数，则Y为800次独立重复试验事件A发生的次数，故Y～B(800，e^-6)，

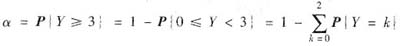，其中

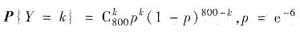，k=0，1，…，n．
由于n=800，p=e^-6，λ=ηp=800×e^-6≈2，根据泊松定理有

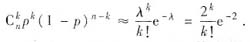
所以α的近似值为

又由于Y～B(800，e^-6)，根据中心极限定理知Y近似服从正态分布N(np，np(1-p))=N(2，2)，所以α的近似值为

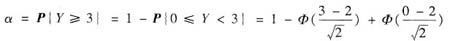
=1-Ф(0.707)+Ф(-1.41)=0.3182．