问题
解答题
| 已知△ABC中,∠C=90°,AC=8cm,BC=6cm,动点P从C点出发,以每秒1cm的速度,沿CA、AB运动到B点. (1)设点P从点C开始运动的路程为xcm,△BCP面积是ycm2,把y表示成x的函数; (2)是否存在点P,使S△BCP=
|
答案
(1)①当0<x≤8时,即当0<P点在AC上,
∴PC=x,
∵∠ACB=90°,BC=6cm,
∵△BCP的面积为ycm2,
∴y=
BC•x,1 2
即y=3x;
②当8<x<18时,P点在AB上,
∵∠ACB=90°,BC=6cm,AC=8cm,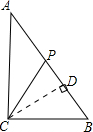
∴AB=10,
∴BP=18-x,
作CD⊥AB,
∴△ABC∽△CBD,
∴AC:CD=AB:BC,
∴CD=
,24 5
∵△BCP的面积为ycm2,
∴y=(18-x)•
×24 5
,1 2
∴y=-
(18-x);12 5
(2)∵BC=6cm,AC=8cm,
∴△ABC的面积=24cm2,
∴△BCP的面积为:24×
=6,1 4
①P点在AB上,
∴6=-
(18-x)12 5
解得:x=
,31 2
∵点P从C点出发的速度为1cm/秒,
∴
÷1=31 2
秒,31 2
∴从C点出发
秒钟时,△BCP的面积为△ABC的31 2
;1 4
②P点在AC上,
∴6=3x,
∴x=2,
∵点P从C点出发的速度为1cm/秒,
∴2cm÷1cm/秒=2秒,
∴从C点出发2秒钟时,△BCP的面积为△ABC的
,1 4
答:从C点出发2秒或
秒钟时,△BCP的面积为△ABC的31 2
.1 4

