| 我们把具有以下性质的函数f(x)称为“好函数”:对于在f(x)定义域内的任意三个数a,b,c,若这三个数能作为三角形的三边长,则f(a),f(b),f(c)也能作为三角形的三边长.现有如下一些函数: ①f(x)=
②f(x)=1-x,x∈(0,
③f(x)=ex,x∈(0,1) ④f(x)=sinx,x∈(0,π). 其中是“好函数”的序号有______. |
任给三角形,设它的三边长分别为a,b,c,不妨设c是最大边,且a+b>c
①f(x)=
,∵x
+a
>b
>a+b
,∴函数f(x)是“好函数”;c
②f(x)=1-x,∵f(a)+f(b)-f(c)=1+c-(a+b),a,b,c∈(0,
),∴f(a)+f(b)-f(c)>0,∴f(a)+f(b)>f(c),∴函数f(x)是“好函数”;1 2
③f(x)=ex,ea+eb>2
=2ea+b
,若2ec
>ec,即ec<4,∵c∈(0,1),∴结论成立,∴函数f(x)是“好函数”;ec
④f(x)=sinx,若f(a)+f(b)=sina+sinb=2sin
cosa+b 2
>sinc,则∵x∈(0,π),-π<a-b<c,∴结论不一定成立,∴函数f(x)不是“好函数”;a-b 2
故答案为:①②③

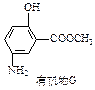
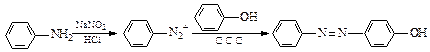
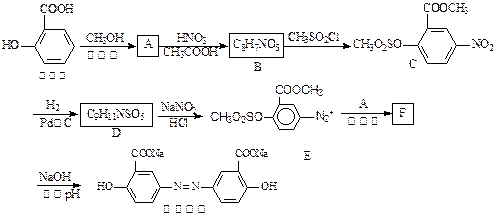
 -氨基酸,能与FeCl3发生显色反应,其分子中共有6种化学环境不同的H原子。X的结构简式为________________
-氨基酸,能与FeCl3发生显色反应,其分子中共有6种化学环境不同的H原子。X的结构简式为________________