问题
解答题
已知⊙O的半径OA=2,弦AB,AC的长分别2
|
答案
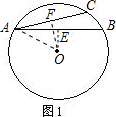
(1)当圆心O在AB、AC的同一侧时,如图1所示,
过点O作OE⊥AB于E,OF⊥AC于F,
由垂径定理得,AE=
AB=1 2
,AF=3
AC=1 2
,2
在Rt△AOE中,cos∠OAE=
,所以∠OAE=30°,3 2
在Rt△AOF中,cos∠OAF=
,所以∠OAF=45°,2 2
所以∠BAC=∠OAF-∠OAE=45°-30°=15°.
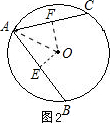
(2)当圆心O在AB、AC之间时,如图2所示,
过点O作OE⊥AB于E,OF⊥AC于F,
同样可得,∠OAE=30,∠OAF=45°,
∴∠BAC=∠OAF+∠OAE=45°+30°=75°.
综上所述,∠BAC的度数为15°或75°.