问题
填空题
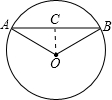
AB是⊙O的弦,半径OA=20cm,∠AOB=120°,则△AOB的面积是______cm2.
答案
过O作OC⊥AB,交AB于点C,如图所示,
则C为AB的中点,即AC=BC,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
在Rt△AOC中,OA=20cm,∠A=30°,
∴OC=
OA=10cm,1 2
根据勾股定理得:AC=
=10OA2-OC2
cm,3
∴AB=2AC=20
cm,3
则S△AOB=
AB•OC=1 2
×201 2
×10=1003
cm2.3
故答案为:1003