问题
解答题
是否存在某个实数m,使得方程x2+mx+2=0和x2+2x+m有且只有一个共同根;如果存在,求出这个实数m及两个方程的公共根,如果不存在,说明理由。
答案
解:假设存在实数m,使这两个方程有且只有一个公共实数根a,由方程根的定义,得

(1)-(2)得:(m-2)a+(2-m)=0,
解得:m=2,或a=1,
当m=2时,两个已知方程为同一方程,且没有实数根,
所以,m=2舍去,
当a=1时,代入(1)得m=-3,当m=-3时,求得第一个方程的根为

第二个方程的根为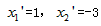
所以,存在符合条件的m,当m=-3时,两个方程有且只有一个公共根x=1。