问题
填空题
平面内有四个点A、O、B、C,其中∠AOB=120°,∠ACB=60°,AO=BO=2,则满足题意的OC长度为整数的值可以是______.
答案
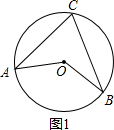
如图1,∵∠AOB=120°,∠ACB=60°,
∴∠ACB=
∠AOB=60°,1 2
∴点C在以点O为圆心的圆上,且在优弧AB上.
∴OC=AO=BO=2;
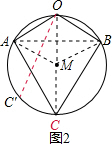
如图2,∵∠AOB=120°,∠ACB=60°,
∴∠AOB+∠ACB=180°,
∴四个点A、O、B、C共圆.
设这四点都在⊙M上.点C在优弧AB上运动.
连接OM、AM、AB、MB.
∵ ∠ACB=60°,
∠ACB=60°,
∴∠AMB=2∠ACB=120°.
∵AO=BO=2,
∴∠AMO=∠BMO=60°.
又∵MA=MO,
∴△AMO是等边三角形,
∴MA=AO=2,
∴MA<OC≤2MA,即2<OC≤4,
∴OC可以取整数3和4.
综上所述,OC可以取整数2,3,4.
故答案是:2,3,4.