问题
解答题
以O为圆心,1为半径的圆内有一定点A,过A引互相垂直的弦PQ,RS.求PQ+RS的最大值和最小值.
答案
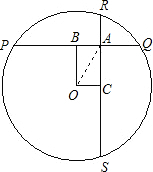
如图,设OA=a(定值),
过O作OB⊥PQ,OC⊥RS,B、C为垂足,
设OB=x,OC=y,0≤x≤a,(0≤y≤a),
且x2+y2=a2.
所以PQ=2PB=2
,1-x2
RS=2(
+1-x2
).1-y2
所以PQ+RS=2(
-1-x2
).1-y2
∴(PQ+RS)2=4(2-a2+2
)1-a2+x2y2
而x2y2=x2(a2-x2)=-(x2-
)2+a2 2
.a4 4
当x2=
时,a2 2
(x2y2)最大值=
.a4 4
此时PQ+RS=
;4(2-a2+2-a2)
当x2=0或x2=a2时,(x2y2)最小值=0,
此时(PQ+RS)最小值=2(1+
).1-a2