问题
选择题
已知定义域为R的函数f(x),对任意的x∈R都有f(x+1)=f(x-
|
答案
因为f(
)=1,所以当x=1时,f(1-1 2
)=f(1 2
)=1此时f(1+1)=f(1-1 2
)+2=3.即f(2)=3;1 2
同理,当x=
时,f(5 2
-5 2
)=f(2)=3,此时f(1 2
+1)=f(5 2
-5 2
)+2=5,即f(1 2
)=5.7 2
当x=4时,f(4-
)=f(1 2
)=5,此时f(4+1)=f(4-7 2
)+2=7,即f(5)=71 2
依此类推,得f(62)=83
故选D

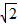 sinl00πt(V),则下列说法中正确的是( )
sinl00πt(V),则下列说法中正确的是( ) V
V