问题
填空题
过圆内某点的所有弦长,长度最短的叫这点的极小弦.则圆内某点的极小弦与该圆过该点的半径______,并且弦长被该点______.
答案
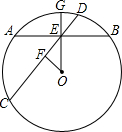
如图,AB,CD是过⊙O内点E的两条弦,
其中AB垂直于半径OG,CD与OG不垂直,
过O作OF⊥CD,则CF=FD,AE=EB,
由勾股定理有:EB2=OB2-OE2,CF2=OC2-OF2,
∵OC=OB OE>OF,∴EB<CF,即AB<CD.
∴极小弦与过该点的半径垂直,并且弦长被该点平分.
故答案是:垂直,平分.