问题
单项选择题
设f(x)的二阶导数f"(x)存在,则求极限
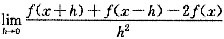 正确的方法是
正确的方法是
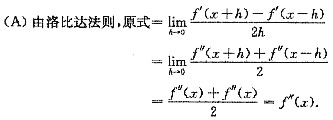
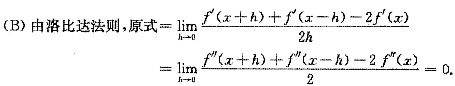
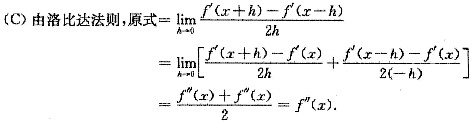

答案
参考答案:C
解析:
[分析]: (A)错.这是因为题设只说f"(x)存在,并未说明f"(x)连续,所以等式
[*]
皆未必成立.
(B)错.此极限中,h是变量,而x是不变量,故使用洛比达法则时,分子、分母均应对变量h求导.此解错在分子是对x求导,而分母是对h求导.
(D)错.事实上,这种解法运用的是乘积的求极限法则,但因[*]不存在,故不能使用乘积的求极限法则。
(C)对.因为这符合导数的定义.
