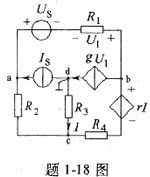
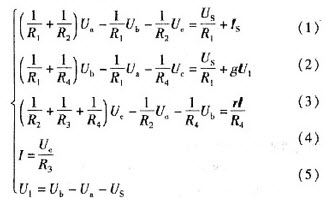A是椭圆长轴的一个端点,O是椭圆的中心,若椭圆上存在一点P,使∠OPA=
|
设椭圆的方程为
+x2 a2
=1,设 A (a,0),点P(acost,bsint).y2 b2
由题意得,
•PO
=0,∴(-acost,-bsint)•(a-acost,-bsint)=0,PA
∴(-acost )•(a-acost )+b2sin2t=0,化简可得 c2cos2t-a2cost+a2-c2=0,
∴e2cos2t-cost+1-e2=0,∴e2=
.1 1+cost
又∵0<e<1,0<1+cost<2,∴
<e2<1,∴1 2
<e<1,2 2
故答案为
<2 2
<1.c a