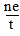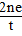问题
解答题
| 已知f(x)是定义在R上的函数,f(1)=1,且∀x1,x2∈R,总有f(x1+x2)=f(x1)+f(x2)+1恒成立. (Ⅰ)求证:f(x)+1是奇函数; (Ⅱ)对∀n∈N*,有an=
(Ⅲ)求F(n)=an+1+an+2+…+a2n(n≥2,n∈N)的最小值. |
答案
(1)证明:f(x1+x2)=f(x1)+f(x2)+1,
令x1=x2=0得f(0)=-1,再令x1=x,x2=-x,得f(0)=f(x)+f(-x)+1
∴f(-x)+1=-[f(x)+1],
函数f(x)+1是奇函数.
(2)令x1=n,x2=1得f(n+1)=f(n)+2,所以f(n)=2n-1,an=
,bn=2×1 2n-1
-1+1=1 2n+1
,1 2n
∴anan+1=
=1 (2n-1)(2n+1)
(1 2
-1 2n-1
)1 2n+1
Sn=
(1-1 2
)=1 2n+1 n 2n+1
又
=(2n-1)bn an
,1 2n
Tn=1×
+3×1 2
+…+(2n-1)1 22
①1 2n
Tn=1×1 2
+3×1 22
+…+(2n-1)1 23
②1 2n+1
由①-②得出
Tn=1 2
+(1 2
+1 2
+… +1 22
)-(2n-1)1 2n-1 1 2n+1
=
+(1-1 2
)-(2n-1)1 2n-1 1 2n+1
计算整理得出得
Tn=3-2n+3 2n
(3)∵F(n+1)-F(n)=a2n+1+a2n+2-an+1=
>01 (4n+1)(4n+3)(2n+1)
∴F(n+1)>F(n).又n≥2,
∴F(n)的最小值为F(2)=a3+a4=12 35