解法一：y=x²+ax-3a的对称轴是x=-

a

2

．

①当-

a

2

≥1，即a≤-2时，x=-1离对称轴最远，而函数开口向上，所以有最大值，

其最大值是a＞

1

4

，与a≤-2相矛盾．

∴a∈∅；

②当-1＜-

a

2

＜1，即-2＜a＜2时，

x=-1或x=1时，有最大值．

由①知，x=-1有最大值时，其最大值是a＞

1

4

，故

1

4

＜a＜2；

当x=1有最大值时，其最大值是1-2a＜0，即a＞

1

2

，故

1

2

＜a＜2．

∴

1

2

＜a＜2；

③当-

a

2

≤-1，即a≥2时，

x=1时有最大值，

其最大值是1-2a＜0，a＞

1

2

，

∴a≥2．

综上所述，a＞

1

2

．

故选B．

解法二：设f（x）=x²+ax-3a，

∵对任意实数x∈[-1，1]，不等式x²+ax-3a＜0恒成立，

∴

f(-1)=1-a-3a＜0 f(1)=1+a-3a＜0

，

即

1-4a＜0 1-2a＜0

，

∴

a＞ 1 4 a＞ 1 2

，故a＞

1

2

．

故选B．
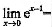