解：（1）一元二次方程x²+（2m-1）x+m²=0有两个实数根，

∴△=（2m-1）²-4×1×m²=-4m+1≥0，

∴m≤；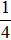

（2）当x₁²-x₂²=0时，即（x₁+x₂）（x₁-x₂）=0，

∴x₁-x₂=0或x₁-x₂=0

当x₁+x₂=0，依据一元二次方程根与系数的关系可得x₁+x₂=-（2m-1）

∴-（2m-1）=0，

∴m=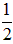

又∵由（1）一元二次方程x²+（2m-1）x+m²=0有两个实数根时的取值范围是m≤，

∴m=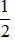不成立，故m无解；

当时x₁-x₂=0，x₁=x₂，方程有两个相等的实数根，

∴△=（2m-1）²-4×1×m²=-4m+1=0，

∴m=

综上所述，当x₁-x₂=0时，m=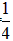。