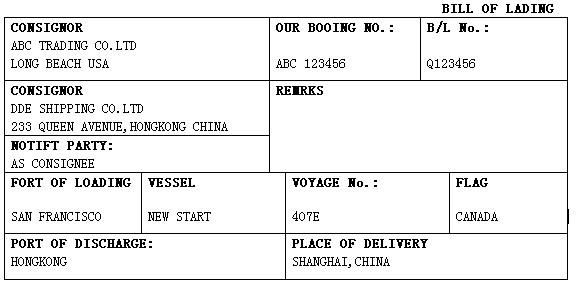
已知函数f(x)=lnx-
(1)当a=1时,判断f(x)的单调性; (2)若g(x)在其定义域内为增函数,求正实数a的取值范围; (3)设函数h(x)=x2-mx+4,当a=2时,若∃x1∈(0,1),∀x2∈[1,2],总有g(x1)≥h(x2)成立,求实数m的取值范围. |
(1)当a=1时,f(x)=lnx-
,1 x
∴f′(x)=
+1 x
=1 x2
,x>0.x+1 x2
∵x>0,∴f′(x)>0,
∴f(x)在(0,+∞)上是增函数.
(2)∵f(x)=lnx-
,g(x)=f(x)+ax-6lnx,a>0.a x
∴g(x)=ax-
-5lnx,x>0a x
∴g′(x)=a+
-1 x2
=5 x
,ax2-5x+a x2
若g′(x)>0,可得ax2-5x+a>0,在x>0上成立,
∴a>
=5x x2+1
,5 x+ 1 x
∵
≤5 x+ 1 x
=5 2 1
(x=1时等号成立),5 2
∴a>
.5 2
(3)当a=2时,g(x)=2x-
-5lnx,2 x
h(x)=x2-mx+4=(x-
)2+4-m 2
,m2 4
∃x1∈(0,1),∀x2∈[1,2],总有g(x1)≥h(x2)成立,
∴要求g(x)的最大值,大于h(x)的最大值即可,
g′(x)=
=2x2-5x+2 x2
,令g′(x)=0,(2x-1)(x-2) x2
解得x1=
,x2=2,1 2
当0<x<
,或x>2时,g′(x)>0,g(x)为增函数;1 2
当
<x<2时,g′(x)<0,g(x)为减函数;1 2
∵x1∈(0,1),
∴g(x)在x=
处取得极大值,也是最大值,1 2
∴g(x)max=g(
)=1-4+5ln2=5ln2-3,1 2
∵h(x)=x2-mx+4=(x-
)2+4-m 2
,m2 4
若m≤3,hmax(x)=h(2)=4-2m+4=8-2m,
∴5ln2-3≥8-2m,∴m≥
,11-5ln2 2
∵
>3,故m不存在;11-5ln2 2
若m>3时,hmax(x)=h(1)=5-m,
∴5ln2-3≥5-m,∴m≥8-5ln2,
实数m的取值范围:m≥8-5ln2;