一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应时间△t的比值定义为角加速度β.我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出)
①如图甲所示,将打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔,然后固定在圆盘的侧面,当圆盘转动时,纸带可以卷在圆盘侧面上;
②接通电源,打点计时器开始打点,启动控制装置使圆盘匀加速转动;
③经过一段时间,圆盘停止转动和打点,取下纸带,进行测量.(计算结果 保留3位有效数字).
(1)用20分度的游标卡尺测得圆盘的直径如图乙所示,圆盘的半径r为______.cm;
(2)由图丙可知,打下计数点D时,圆盘转动的角速度为______rad/s;
(3)纸带运动的加速度大小为______m/s2,圆盘转动的角加速度大小为______.rad/s2.
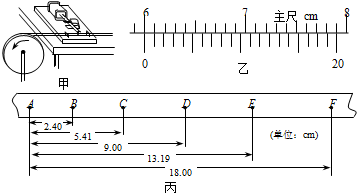
(1)整数部分为60mm,小数部分为零,由于精确度为0.05mm,故需写到0.001cm处,故读数为6.000cm;故半径为3.000cm;
(2)打下计数点D时,速度为
vD=
=CE 2T
=0.389m/s(13.19-5.41)×0.01 2×0.1s
故
ω=
=v r
≈6.5rad/s0.389 0.06
(3)纸带运动的加速度为
a=
=△x (△t)2
=CE-AC (△t)2
=0.593m/s2(13.19-2×5.41)×0.01 0.22
由于β=
,ω=△ϖ △t
,故角加速度为β=v r
=a r
≈19.8rad/s20.59 0.03
故答案为:(1)3.000cm;(2)13.0rad/s;(3)0.593(0.600)m/s2,19.8(20.0)rad/s2.
