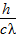问题
解答题
已知f(x)=
(1)当a=4时,求F(x)的最小值 (2)当1≤x≤4时,不等式F(x)>1恒成立,求a的取值范围. |
答案
(1)当a=4时,F(x)═
=4(4x+16- x x
+x
)-1≥4•24 x
-1=15∴当4
=x
,即x=4时,F(x)min=15(4分)4 x
(2)F(x)=
=ag(x)-f(x) f(x)
=a(a(x+a)- x x
+x
)-1,x∈[1,4](6分)a x
设t=
,则F(x)=a(t+x
)-1,t∈[1,2],令h(t)=a(t+a t
)∵F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数y=x+a t
的单调性知a x
或
>2a h(t)min=h(2)>2
或1≤
≤2a h(t)min=h(
)>2a 0<
<1a h(t)min=h(1)>2
或a>4 a(2+
)>2a 2
或1≤a≤4 2a
>2a
,解得a>1(12分)0<a<1 a(1+a)>2

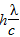 ,m=0
,m=0 ,m=
,m=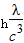
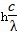 ,m=0
,m=0 ,m=
,m=