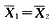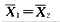∵点P为椭圆C：

x2

4

+

y2

b2

=1 （b＞0）上的动点，

∴设P（2cosα，bsinα），可得

|OP|²=4cos²α+b²sin²α=

1

2

（b²+4）+（2-

1

2

b²）cos2α

∵|OP|的最小值为1，得|OP|²的最小值也为1

∴

1

2

（b²+4）-|2-

1

2

b²|=1

当b²≥4时，方程化为

1

2

（b²+4）-（

1

2

b²-2）=1得4=1，无实数解；

当b²＜4时，

1

2

（b²+4）-（2-

1

2

b²）=1，即b²=1，解之得b=1

综上所述，所求b的值为1

故答案为：1