问题
解答题
已知关于x的一元二次方程x2+(m-1)x-2m2+m=0(m为实数)有两个实数根x1、x2。
(1)当m为何值时,x1≠x2;
(2)若x12+x22=2,求m的值。
答案
解:(1)△=(m-1)2-4(-2m2+m)
=m2-2m+1+8m2-4m
=9m2-6m+1
=(3m-1)2
要使x1≠x2 ,
∴△>0,即△=(3m-1)2>0
∴m≠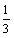 。
。
(2)∵x1=m,x2=1-2m,x12+x22=2
∴m2+(1-2m)2=2
解得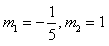 。
。
