问题
解答题
在平面直角坐标系中,已知点O(0,0)、A(1,n)、B(2,0),其中n>0,△OAB是等边三角形.点P是线段OB的中点,将△OAB绕点O逆时针旋转60°,记点P的对应点为点Q,则n=______,点Q的坐标是______.
答案
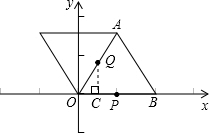
∵O(0,0)、B(2,0),
∴OB=2,
∵△OAB是等边三角形,点P是线段OB的中点,
∴OP=
OB=1,1 2
∴n=
AO=3 2
×2=3 2
,3
根据旋转变换的性质,OQ=OP=1,
过点Q作QC⊥OB于点C,
则OC=OQ?cos60°=1×
=1 2
,1 2
QC=OQ?sin60°=1×
=3 2
,3 2
∴点Q的坐标为(
,1 2
).3 2
故答案为:
,(3
,1 2
).3 2
