等比数列{xn}各项均为正值,yn=2logaxn(a>0且a≠1,n∈N*),已知y4=17,y7=11
(1)求证:数列{yn}是等差数列;
(2)数列{yn}的前多少项的和为最大?最大值是多少?
(3)求数列{|yn|}的前n项和.
(1)∵{xn}是等比数列,设其公比为q,
=q(定值),yn+1-yn=2(logaxn+1-logaxn)=2logaq(是定值),xn+1 xn
所以数列{yn}是等差数列. 4'
(2)由(1)知{yn}是等差数列,y7=y4+3d即 11=17+3d
∴d=-2,yn=17+(n-4)d=25-2n6'
由25-2n≥0得n≤25 2
当n≤12时yn>0;当n≥13时,yn<0所以数列{yn}的前12项和最大;
∵y1=23,
∴最大值S12=12×23+
(-2)=144; 9′12×11 2
(3)Sn=23n+
(-2)=24n-n2设{|yn|}的前n项和为Tn,n(n-1) 2
∵当n≤12时yn>0;当n≥13时,yn<0,
∴当1≤n≤12时 Tn=Sn=24n-n211′
当n≥13时,Tn=a1+a2+…+a12-a13-…-an=S12-(Sn-S12)=2S12-Sn=2×144-24n+n213′
所以Tn=
(n∈N*) 14'24n-n2 (1≤n≤12) n2-24n+288 (n≥13)

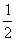 ,则所得图形的面积与原来图形的面积( )。
,则所得图形的面积与原来图形的面积( )。