问题
填空题
已知A(4,0),B(2,2),M为椭圆
|
答案
椭圆
+x2 25
=1中a=5,b=3,所以c=4,所以A为椭圆的焦点y2 9
设M到右准线的距离为d,则由椭圆的第二定义可得,
=|MA| d 4 5
∴d=
|MA|5 4
∴
|MA|+|MB|=d+|MB|5 4
∴MB垂直于准线时,
|MA|+|MB|取得最小值5 4
∵右准线方程为x=
=a2 c 25 4
∴
|MA|+|MB|的最小值为5 4
-2=25 4 17 4
故答案为:17 4

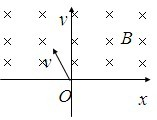
 v/aB,正电荷
v/aB,正电荷 v/aB,负电荷
v/aB,负电荷