问题
解答题
设α,β是关于方程x2 -2(k-l)x+k+1=0的两个实根,求y=α2+β2关于k的解析式,并求y的取值范围.
答案
解:根据根与系数的关系有α+ β=2(k-1) , αβ=k+1 ,
∴y= α2+ β2=( α+ β)2-2 αβ=[2(k-1)]2-2(k+1)= 4k2-10k+2 ,
∵一元二次方程有两个实根,
∴△≥0 ,得k ≥3 或k ≤0 ,
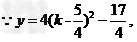
∴y≥2.
设α,β是关于方程x2 -2(k-l)x+k+1=0的两个实根,求y=α2+β2关于k的解析式,并求y的取值范围.
解:根据根与系数的关系有α+ β=2(k-1) , αβ=k+1 ,
∴y= α2+ β2=( α+ β)2-2 αβ=[2(k-1)]2-2(k+1)= 4k2-10k+2 ,
∵一元二次方程有两个实根,
∴△≥0 ,得k ≥3 或k ≤0 ,
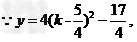
∴y≥2.