问题
问答题
确定常数a,使向量组a1=(1,1,a)T,a2=(1,a,1)T,a3=(a,1,1)T可由向量组β1===(1,1,a)T,β2=(-2,a,4)T,β3=(-2,a,a)T线性表示,但向量组β1,β2,β3不能由向量组a1,a2,a3线性表示.
答案
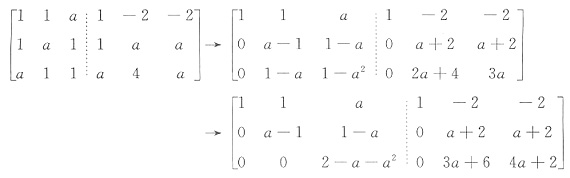
参考答案:由已知得,β1,β2,β3不能由向量组a1,a2,a3线性表示,所以方程组x1a1+x2a2+x3a3=βj(j=1,2,3)无解.对增广矩阵作初等行变换,有
a=1时,
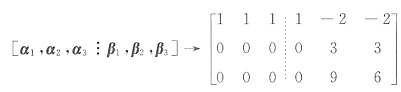
显然a1,a2,a3可由β1,β2,β3线性表出,但β2,β3不能由a1,a2,a3线性表出,即向量组β1,β2,β3不能向a1,a2,a3线性表出.
a=2时,
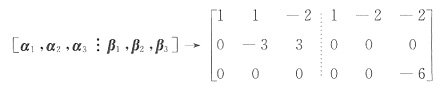
向量组a1,a2,a3组不能由β1,β2,β3组线性表出,β1,β2,β3组也不能由a1,a2,a3线性表出.
a≠1,a≠-2时,r(a1,a2,a3)=r(β1,β2,β3)=3,可相互表出,
故知a=1时,满足题设要求.
