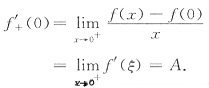问题
问答题
证明:若函数f(x)在x=0处连续,在(0,δ)(δ>0)内可导,且[*],则f’+(0)存在,且f’+(0)=A.
答案
参考答案:根据右导数的定义,要证函数f(x)在x=0点的右导数存在,只需要讨论
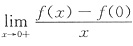 .
.
方法一:利用求极限的洛必达法则
当x→0+时
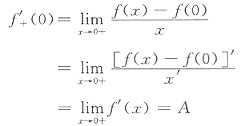
方法二:利用拉格朗日中值定理
对于任意的x∈(0,δ),函数F(x)在闭区间[0,x]上连续,在开区间(0,x)内可导,则有
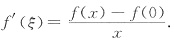
而x→0+时,ξ→0+,