已知y[1]=e[3x]-xe[2x]，y[2]=e[x]-xe[2x]，y[3]=

搜题请搜索小程序“爱下问搜题”

问题填空题

已知y[₁]=e[^3x]-xe[^2x]，y[₂]=e[^x]-xe[^2x]，y[₃]=-xe[^2x]是某2阶常系数非齐次线性微分方程的3个解，则该方程满足条件

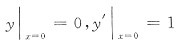的解y=______．

答案

参考答案：e^3x-e^x-xe^2x

解析： y₁-y₂=e^3x-e^x，y₂-y₃=e_x是对应齐次微分方程的解．
由分析知，y^"=-xe^2x是非齐次微分方程的特解．
故原方程的通解为y=C₁(e^3x-e^x)+C₂e^x-xe^2x，C₁C₂为任意常数．
由

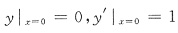可得C₁=1，C₂=0．
通解为y=e^3x-e^x-Xe^2x．

解答题

我市樊城区太平店镇有一株“千年银杏树”，是迄今为止我市发现的最古老的一棵树，距今已有一千九百多年，依然枝繁叶茂，树干高达10米．根据你所学的知识，完成下列问题：

（1）银杏树是裸子植物，种子外无______包被．种子中贮存的有机物来自叶的______作用．

（2）银杏树是雌雄异株植物，雄株不结种子．如果想让雄株结种子，你认为以下哪种方法最可行______．

A．扦插 B．压条 C．人工受粉 D．嫁接

（3）银杏树虽然高达10米，但其顶部水分充足．根吸收的水分通过______运输到顶部．

（4）高大的银杏树也成了鸟类的栖息地，鸟类在那里筑巢、育雏．从获得途径上来看，鸟类的育雏行为属于______行为．保护生物的栖息地，保护______，是保护生物多样性的根本措施．

单项选择题

甲氨蝶呤主要用于（）

A．消化道肿瘤

B．儿童急性白血病

C．慢性粒细胞性白血病

D．恶性淋巴瘤

E．肺癌